 |
||||
Okay, you finally 'get' linear equations, right? The next thing that comes up in algebra is when you have TWO or MORE linear equations. This is called a SYSTEM of equations. (Yeah, you'd think it would be a set of equations, but, no, it's a system.) And, like anything else, there is more than one way to solve these systems. So, let's take a look at how we can solve these systems of equations. |
||
Let's start with an easy (ha!) way to solve a system of equations…the Graphing Method! You need some graph paper, a straight-edge (a ruler will work), and a pencil. If you have two color pencils, that would be nice, too. We will need our two equations: |
||
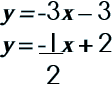 |
 |
|||||
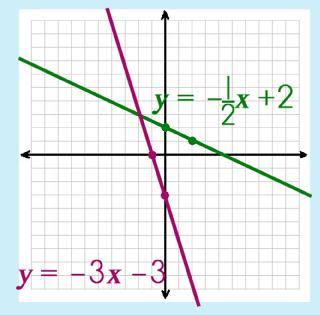
Step 1: Graph each line. (use a different color pencil, to help you see each line)
|
||||||
 |
||||||
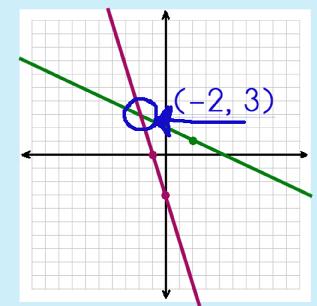
Step 2: Find the point of intersection. Circle it.
|
||||||
Step 3: Double-check your solution.
|
||||||
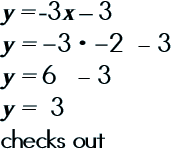 |
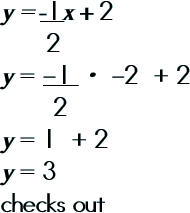 |
|||
But wait! What if there is NO solution? Could this happen? Of course! Sometimes the lines might be parallel! Then, of course, there will be no solution! You could also have a case where the lines are the same, i.e., they have the same slope and same y-intercept! In this case, the solution set is infinite. |
||
 |
||||
 |
||||
Your solution set can have
|
||
Great! We've got the ball rolling now so let's try another method for solving systems of equations…the Substitution Method. Sounds easy, right? You're used to using this method so it should be a piece of cake! Let's use some new equations (and then you can go back at the very end and try all of 'em with the different methods for fun). |
||
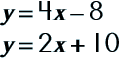 |
||
Step 1: Choose one of the equations and subsitute the other equation for one of the variables.
|
||||
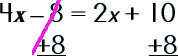 |
||||
Step 2: Solve for the one variable.
|
||||
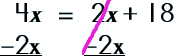 |
||
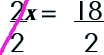 |
||
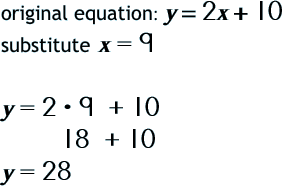 |
||||
Step 3: Now, go back, substitute this value into one of the equations and solve for the other variable.
|
||||
Step 4: Double-check by substituting your coordinate pair (solution set) with the other equation.
|
||||
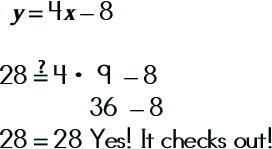 |
||||
 |
||
Now, you must admit, this systems of equations stuff isn't all that hard, right? So, are you ready for the last method? The Elimination Method isn't magic but it is a great way to show how one of those 'properties' that we are always memorizing works for us. It's the Equality property (if a = b and c = d then a + c = b + d…). This method is a bit more, shall we say intense for some folks, but can be extremely useful so we'll start out with an easy one and then do a more 'challenging' one. |
||
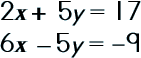 |
||
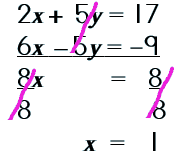 |
||||
Step 1: Set up the equations vertically as an addition problem.
|
||||
Step 2: Solve for the one variable. |
||||
Step 3: Now, go back, substitute this value into one of the equations and solve for the other variable.
|
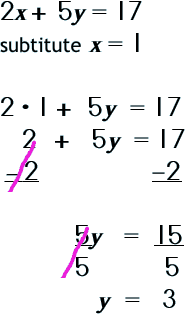 |
|||
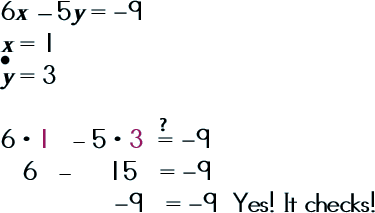 |
||||
Step 4: Double-check by substituting your coordinate pair (solution set) with the other equation.
|
||||
As promised, here are the same problems from each section but time to try 'em out with the other methods. |
||
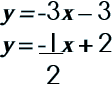 |
||||
Use the Substitution Method to solve this system of equations.
|
||||
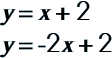 |
||||
Use the Graphing Method to solve this system of equations. |
||||
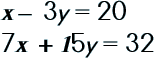 |
||||
Use the Elimination Method to solve this system of equations.
|
||||
EEK! None of the variables can cancel out as is. This means we need to MAKE one of them do so…by going an extra step.
We need to make one of the terms into one that can be elimated so I chose to multiply the entire first equation by 5. NOW, we can use the Elimination Method! Yahooooo! |
||||||||
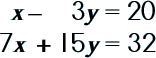 |
||||||||
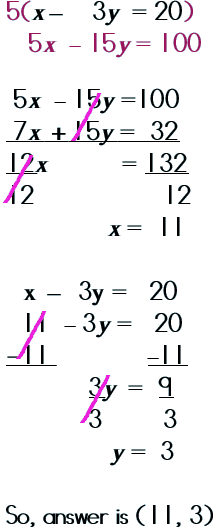 |
||||||||
Go back and substitute x = 11 into an equation… |
||||||||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||