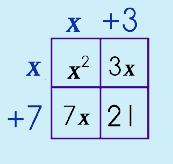 |
||
If you can multiply then you can factor. Why? The skill involved in factoring is basically the skill you need to multiply because factoring is the opposite (a-ha! An inverse operation!) of multiplication. Being able to work through sum and product puzzles provide you the tools and skills needed to factor quadratics! Two different methods will be used: The first utilizes working backwards using the sum and product puzzles followed by the generic rectangle method to come up with the factors. The second method shows how to utilize working backwards from the FOIL method. Both are quite simple, truly. |
||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
Are you whining already? Sheesh! When you say 'hard' are you talking about one of those quadratics where there's a coefficient right from the beginning? Hey, no worries! There's a little trick involved…just an extra step you need to do at the BEGINNING and you already know how to do this extra little step…it's the infamous Sum & Product aka Diamond Puzzle |
||
So, let's say this is our problem… |
||||
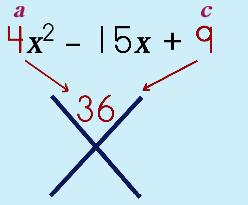 |
||||
Step 1: Make a Sum & Product Puzzle. Put ac at the top.
|
||||
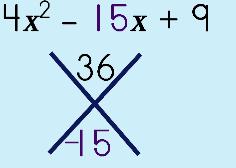 |
||||
Step 2: Put b in the bottom of the puzzle.
|
||||
Step 3: Solve the puzzle. Product on top, sum on bottom
|
||||
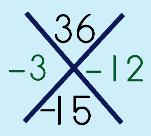 |
||||
 |
||||
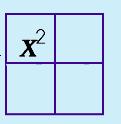
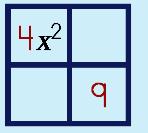
Step 4: Make a Box (generic rectangle). Fill in term a and c.
|
||||
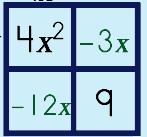 |
||||
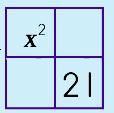
Step 5: Place the Sum & Product numbers in the other two boxes.
|
||||
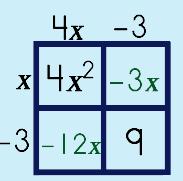 |
||||||||
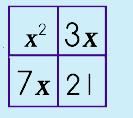
Step 6: Move the factors OUT.
|
||||||||
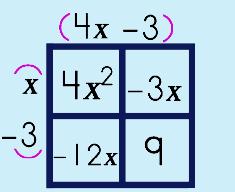 |
||||||||
Step 6: Add parenthesis.
|
||||||||
In this method, we're going to be looking at the trinomial as the product of two binomials. Our goal is to find the binomials that when multiplied give us the trinomial. Follow along… |
||
Here's our trinomial or quadratic: |
||||
Step 1: Set up the two sets of parentheses (-----)(-----) to come up with the FIRST term in each binomial.
|
||||||
Step 2: Now, the goal is to find the products of the LAST term in the trinomial.
|
||||||
Step 3: Consider the MIDDLE term in your trinomial.
|
||||||
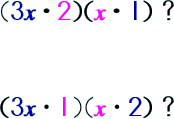 |
||||||
Easy-peasy, lemon-squeasy! |
||||||
|
||||||||||||||||||||||||||||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||