item49
Exponents RationalExpressions BoxMethod QuadraticEquations
PropertiesofEquality FractionsinEquations SumandProductPuzzles StandardFormofQuadraticFunction
LinearEquations SolvingInequalities MultiplyingPolynomials item2a
SquareRootsSquareNumbers HowtoFindSlope SystemsofEquations FactoringPolynomials item3a
PythagoreanTheorem xandyintercepts FactoringTrinomials item5a
border1a
border1a1
border1a1b
Completing the Square

When working with quadratics one of the concepts you will definitely need to learn is something called 'completing the square.' Now those of you who have been in my classes are more than familiar with square numbers because we worked a LOT on memorizing the square roots and squares of numbers, right? NOW, all that work is going to pay off big time!

The idea of 'completing the square' is useful because it helps when you want to re-write a quadratic equation into a form that allows you to apply the square root principle. It is another method that is kind of like factoring but utilizes squares.

Completing the Square when a
x2 + 6x –

Here's a problem:

Step 1: Re-write your problem in the form ax2 + bx = c

 
Use the Equality Property of Addition or Subtraction so that your expression now is in the form ax2 + bx = c
x2 + 6x –

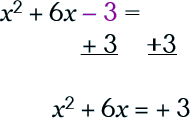Step 2: Take half of b. Now, square it.

Take half of b (in other words, divide the value of b by 2!). Now, square the value.
 
1
(
• b
+ 6
= 3
x2 + 6x

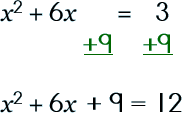Step 3: Add this number to each side of the equation.

Add the number you got in Step 2 to each side of your equation. Simplify.
 
 

Step 4: Write the ax2 +bx +c side as a square.

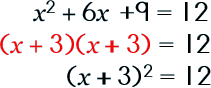Factor the trinomial side as a square i.e., (x + 1)2
 
 

Step 5: Take the square root of each side.

Now, just take the square root of each side of the equals sign. You're done!
 
 
√12 =√4 • √3

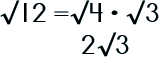remember:
√(x + 3)2 =
Answer
Let's Practice Problems where a

To see how the process is done in a linear, straight-forward way, here are two more examples. See if you can follow along…
DJIMiniBBHootbranchc
DJIMiniBBHootowl1c
x2 + 8x -x2 + 4x –
-x2 + 4x –
x2 + 8x =
8
= 4
x2 + 8x
4
= 2
x2 + 8x +
(x + 4) = (x + 4) =
Answer is
Answer is
Completing the Square when a

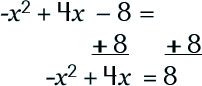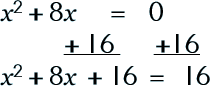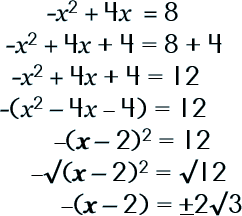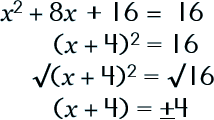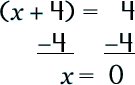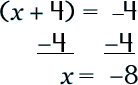Now, when you have a quadratic equation and a is NOT 1, this is when you will want to use some other steps to complete the square. Follow along, please.

Here is a problem:

 3x2 + 18x +

Step 1: Check to see if you can factor out a common factor.

If you are able to factor out a common factor, do it! In this particular problem, it is possible to factor out the 3. (In some practice problems at the bottom of this page, there will be examples where this is not happening so don't worry!)
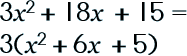3x2 + 18x +
3(x2 + 6x +

Step 2: Ignore the coefficient on the outside of the parenthesis. Re-write your problem in the form ax2 + bx = c

Ignore the coefficient (in this case, the 3). Move the c (+5) to the other side of the equals sign using the Subtraction Property of Equality. Basically, you now follow the same steps as in the flow map above!
x2 + 6x +

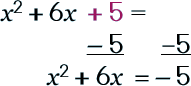Step 3: Take half of b. Now, square it.

Take half of b (in other words, divide the value of b by 2!). Now, square the value.
 
6
= 3

Step 4: Add this number to each side of the equation.

Add the number you got in Step 2 to each side of your equation. Simplify.
x2

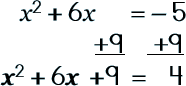Step 5: Write the ax2 +bx +c side as a square.

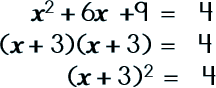Factor the trinomial side as a square i.e., (x + 1)2
 

Step 6: Take the square root of each side.

Now, just take the square root of each side of the equals sign. That's it!
√(x + 3)2 =
(x + 3) (x + 3)
Answer is
Conjugate Pairs

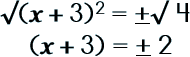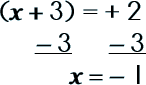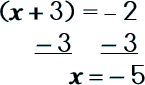What is a conjugate pair? Why, sometimes you may need to rationalize a number and so you will want to learn just how to do this. Conjugate pairs will help you do this. The reason you may want to rationalize a number is like when you have a radical in the denominator…eeewww! Nasty, right? So, to get rid of that nasty ol' radical, use the conjugate pair!

Let's see what a conjugate pair LOOKS like.
a + √b a – √b

is

The conjugate pair of

So, why care about learning about conjugate pairs and what do they have to do with completing the square? Let's put some numbers in to substitute for the variables to see what happens and then multiply!
(7 + √8)(7 – √8)

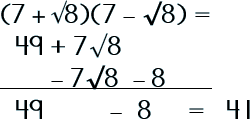Did you see what happened?

It's the difference of two squares! The radicals disappeared!

Yep, and all that was left…rational numbers! WOW… totally cool!

A conjugate pair is a binomial factor together which together with its original forms a product that is the difference of two squares. Wooo, what a mouthful. Basically, they are the sum and difference of the same two terms. (Either way, a mouthful!).

Where can this be used? Why, you can use it to remove radicals from the denominator (I mean, really, who wants to deal with radicals in the denominator, for heaven's sake?). Let's try it.

Say, you have a problem like the following and you are asked to rationalize the denominator. How would you do that?
1

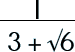Step 1: Multiply by the conjugate pair.

Think of fractions! You are going to multiply the numerator AND denominator by the conjugate pair because by doing so, you are basically multiplying by 1!
(3 – √6)
1
•

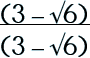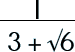Step 2: Simplify.

The radicals will 'disappear' and all that is left will be rational numbers in the denominator. Simplify. Voila!
3 – √6 3 – √6
=

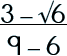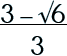©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.
Pythagorean Theorem PythagoreanTheorem