EEK! Mixture Problems! These common algebra problems confuse the heck out of everyone. I think the reason for the confusion is because books teach it using just one variable. It is SO much easier when solved with TWO variables. Seriously! Check it out…

Here's a typical mixture problem:

Kyle has a solution that is 40% acid and a second solution that is 80% acid. He needs to mix some of both solutions to make 300 liters of a solution that is 64% acid. How many liters of each solution will he need to make 300 liters of a 64% acid solution?

How do you go about solving it?

Let's think of it like this:

In order to begin solving the equation, we need to do a bit of work…we have two variables so this is kind of crazy, right? We can easily make a substitution so let's say we solve for y.

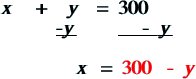Here we solved for x.

Now, just simply substitute the value for x (the 300 – y) for the x in the equation as follows:

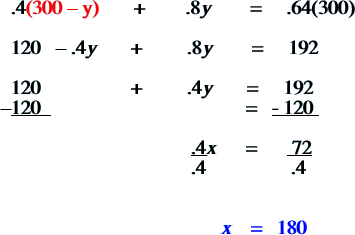Go back and substitute your x value into the original equation…

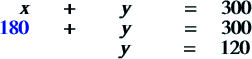So, you can now answer the question! Kyle needs 180 liters of the 40% and 120 liters of the 80% solution! Yahooo!

©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.