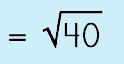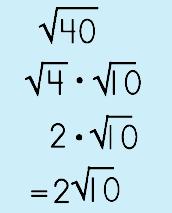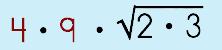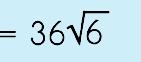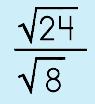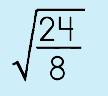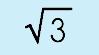|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This is probably the weirdest thing you will deal with when working with radicals but it isn't difficult so don't stress out. All it means when you hear the phrase, "rationalize the denominator' is to turn the radical that is in the denominator into a whole number OR into a rational term. That's it! The way to do it is to use one of my faves…you'll recognize it. |
||
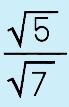 |
||||||||
Step 1: Simplify the denominator (if you can) In this case, it isn't necessary but sometimes you may have to. |
||||||||
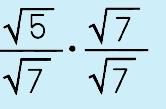 |
||||||||
Step 2: Multiply the numerator and denominator by the RADICAL in the denominator. |
||||||||
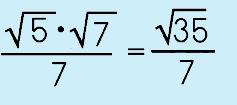 |
||||
Step 3: Simplify the numerator. That's it! You can see that the denominator now becomes the radicand minus the radical sign and there is no radical sign as a denominator. |
||||
 |
||||
Radicals are easy-peasy, lemon-squeasy! |
||||
Sometimes you may need to rationalize a number where the fraction is paired with a radical. You can use a conjugate pair to rationalize the denominator! |
||
|
||||||||||||||||||||
A conjugate pair is a binomial factor together which together with its original forms a product that is the difference of two squares. Wooo, what a moutful. Where can this be used? Why, you can use it to remove radicals from the denominator (I mean, really, who wants to deal with radicals in the denominator, for heaven's sake?). Let's try it. Say, you have a problem like the following and you are asked to rationalize the denominator. How would you do that? |
||
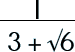 |
||
Step 1: Multiply by the conjugate pair.
|
||||||||
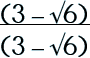 |
||||||||
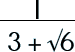 |
||||||||
Step 2: Simplify.
|
||||||||
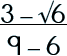 |
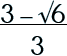 |
|||||||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||