|
|||||||||||||
Positive and negative numbers are rational numbers and terminating decimals are rational numbers. So, what is an irrational number? Ahhh…you know how you had some of those 'weird' fractions that when you divided you just kept getting a non-terminating decimal that was non-repeating? Well, THAT'S an irrational number. So, let's just concentrate, shall we? on the RATIONAL ones (yeah! the ones that kinda make sense?) right now. |
||
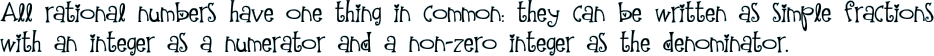 |
||
A rational number is a number that can be written as a fraction where both a and b are integers; b cannot be zero. |
||
where |
||||||
This means that there are basically three types of rational numbers. Let's take a look and see what they are. |
||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
SO, what does this all mean? IF you come across a number that cannot fit any of the three 'rules' then it is probably (drum roll, please) an irrational number! The famous one you will be dealing with is π . *Note: There are some 'other' numbers, like Imaginary numbers but we won't be getting into those… |
||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||


