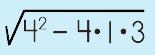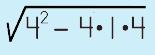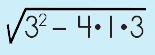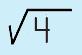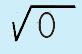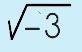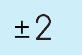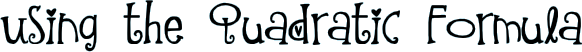Any time you come across a quadratic equation there are several different ways or methods you can actually solve them. One way is to use what's called the 'quadratic formula.' This is probably something your parents will remember from Algebra class (and will be rolling their eyes as they remember it!). The formula has this oddball look to it…

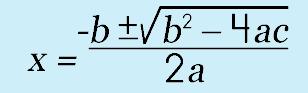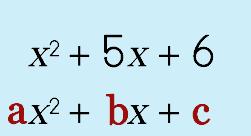Now, you may be thinking, "What in the heck? How do I use THIS thing?" It is actually quite simple! Just think about your quadratic EQUATION for a moment. It looks something like this, right?

Well, then if you would think BACK to when you were first learning about the quadratic equation, you learned that the first term's coefficient is represented by the letter a, the second term is represented by the letter b, and the third by the letter c.

Why is all this so important, you may be wondering, right? The reason this is all so important is because you can find the solution to ANY quadratic equation by using the quadratic formula! WOW…amazing, right? So, it stands to reason that you should memorize this oddball formula. As long as you can remember it and you definitely should have no problem with remembering the 'standard' form of a quadratic equation (hint-hint: the form you see above) then you simply just substitute the values for a, b, and c into the quadratic formula.

Now, keep in mind that I am going to show you what I think is a good way to go about using the formula…someone else may tell you to go about it a different way…

Step 1: Start with your quadratic equation in standard form

If your equation is not in the 'standard' form, then get it into that form!

Standard form is ax² + bx + c

 

Determine your a, b, and c.

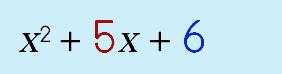Step 2: Use the discriminant to determine the number of solutions you will get

Substitute the values in the discriminant (the expression under the radical sign). This will tell you how many solutions you will ultimately have when you are finished! It will also tell you what your x-intercepts will be.

 

If you get a PERFECT SQUARE, then you will have two solutions. The roots are rational.

If you get a positive number that is not a square, you will have two irrational solutions.

If you get 0, then you have one rational solution.

If you get a negative number, you will have no solution. The roots are imaginary.

A-ha! Perfect square! This means we will have two solutions.

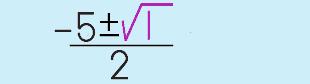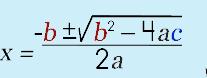Step 3: Substitute each the last two coefficients in the formula.

Put the discriminant solution in (a-ha!).

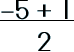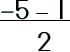Step 4: Simplify

Now, just simplify. The IMPORTANT thing to do is to be VERY careful when you 'do the math.' Carelessness is going to cost you big time…

Step 5: Solution

Remember, the solutions are also the x-intercepts of the corresponding parabola! This means that when y = 0, the solutions you get here are where the graph will intersect the x-axis! Nifty!

Ahhhh…you have come up with that little issue that can be EASILY explained when you understand the discriminant. (For those of you who can find the base word in 'discriminant' you will probably be able to figure out what this is going to get at…)

When you learned about radicals you learned that the number/term under the radical sign is called the radicand. When you are working with the quadratic formula, the expression found under the radical sign is called the discriminant. This is a rather important expression, as you will soon learn. Let's take a look at WHY you want to learn about the discrimant.

©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.