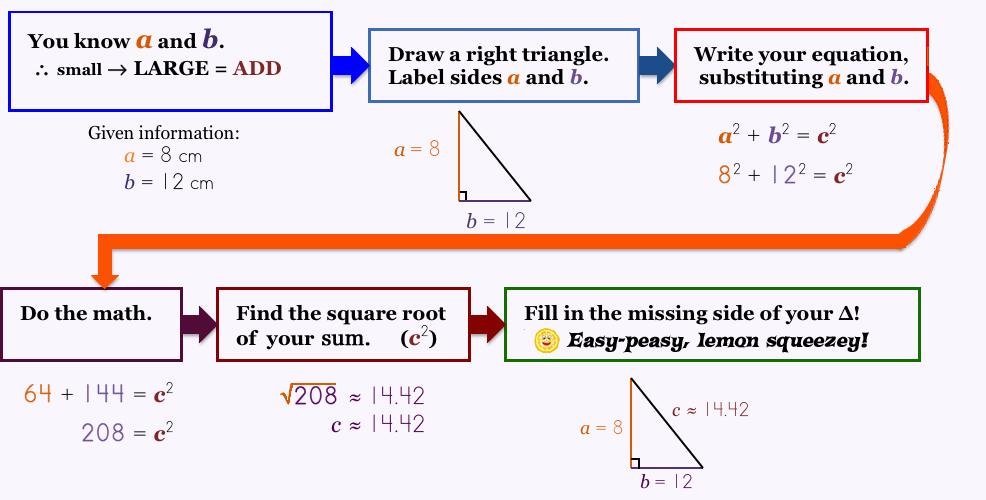
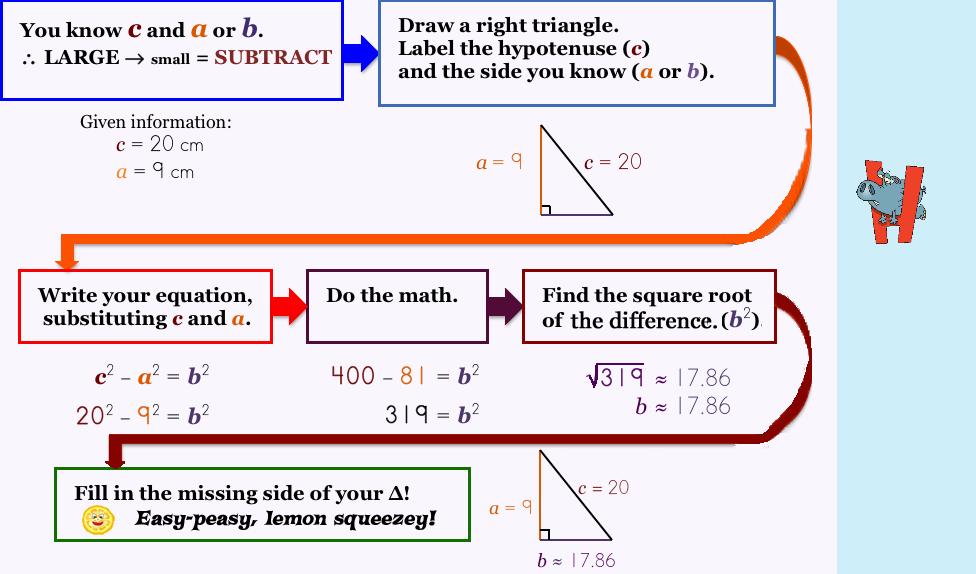
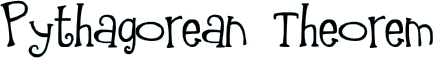|
Pythagoras was a philosopher and religious leader from Samos, an island off of Greece, (between around 570–495 B.C.E.). He became well-known for his developments in mathematics, astronomy, and music theory. A secret group, the Pythagoreans, was formed in the city of Croton where Pythagoras taught a curricula of four mathemata or studies consisting of arithmetica (number theory), geometria (geometry), astrologia (astronomy), and harmonia (music). From this secret brotherhood, which believed, "Brotherhood is the greatest purification," we have learned about the Pythagorean Theorem (although it is highly probable and likely that the theorem has been around for much longer. The Pythagoreans, however, provided the first logical proof of the theorem.
|
|