 |
||
Okay, now here's a concept that may not seem like a big deal but in a lot of ways it IS a big deal. Why? Well, in Algebra, one of the 'big' ideas is that you are always factoring polynomials. If you don't know how to factor a MONOmial, then how in the heck can you possibly factor POLYnomials and quadratics? Finding the factors of monomials is a basic, foundational skill. It goes WAY back to what you learned in elementary school…and the days of the 'greatest common factor' and 'greatest common divisor.' Let's see how you can put that old knowledge to use in Algebra! So, let's say you have two monomials like |
||
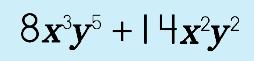 |
||
and, you wanted to find out what the Greatest Common Factor they share is. What would be the best or easiest method for finding it? Check this out! |
||
Step 1: Write out the monomials side-by-side.
|
||||
 |
||||
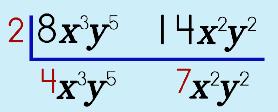
Step 2: Look at the COEFFICIENTS.
|
||||
 |
||||
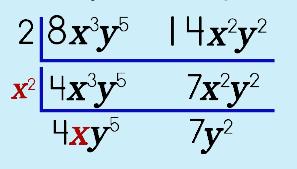 |
||||
Step 3: Look at the first common variable.
|
||||
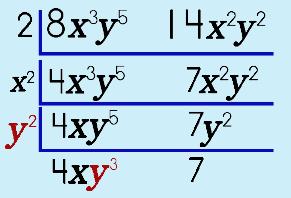 |
||||
Step 4: Continue factoring the variables. Each variable/step has its own floor on the house!
|
||||
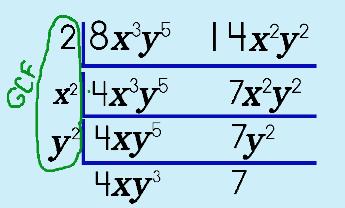 |
||||||
Step 5: Writing the GCF…
|
||||||
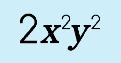 |
||||||
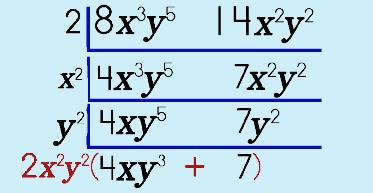 |
||||||||||
Step 6: Put it ALL together now!
|
||||||||||
 |
||||||||||
Easy-peasy, lemon-squeasy! |
||||||||||
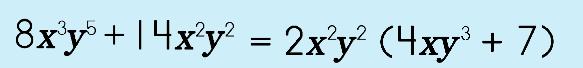 |
||||||||||
When you factor a polynomial you are finding the factors, which are not just numbers but numbers AND variables, that are common to each term in the polynomial. The common factors do not 'disappear' once you factor them out either…because they 'reappear' outside of a set of parentheses! Basically, you are re-arranging terms. |
||
An important thing to remember is that when you factor and 'nothing' is left, there is NEVER 'nothing' left! Why is this? (stop and think about this for a second…) We are talking about multiplicationa and division, right? If we put down a 0 (zero), then what does this mean? Uh oh...it doesn't work. So, if 'nothing' is left, then always put down a 1 (one). See the example to the right. |
||||
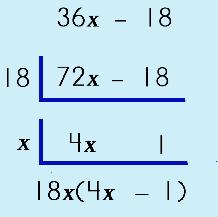 |
||||
©2011–2017 Sherry Skipper Spurgeon. All Rights Reserved. |
||