Back in Pre-Algebra we used a number of properties but never properly identified them. We called things 'inverse' or simply just used the properties but never justified our reasoning when solving for a variable. Now in Algebra, it is important to be able to justify WHY and HOW we get to each step. So, here are some of those properties you've been working with…

Let's start off with a typical 2-step linear equation like this one:

I know you all know how to go about solving for x but let's see how you can use your deductive reasoning skills to actually justify the properties you use as you work through each step. Here we go!

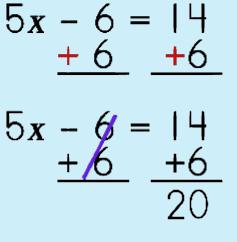Step 1: Addition Property of Equality

Okay, you took the inverse of -6 (the additive inverse) which is +6. This means you ADDED 6, right? Because you are ADDING to BOTH sides of the equals sign, as you are balancing the equation, the property is the Addition Property of Equality.

 

Makes sense.

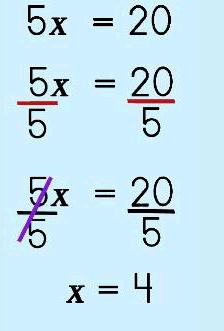Step 2: Division Property of Equality

Next up, you have now simplified things so you are down to 5x = 20.

 

The next step is to find the inverse operation where you can isolate the variable, x, from the 5. Since 5x is the same as multiplying 5 by x the inverse operation is division. This means you will be DIVIDING both sides by the coefficient that is with the x. The property, thus, is the Division Property of Equality.

 

A-ha!

 

Is it really this simple? Yep, it is!

 

Now, we have simplified things and have solved for our x!

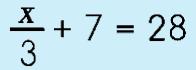I bet you are starting to get the idea behind these 'equality' properties now. Let's see if you are able to follow the steps in the next problem example.

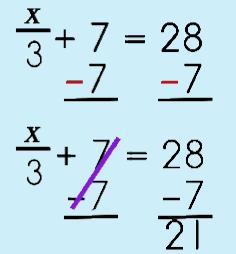Step 1: Subtraction Property of Equality

You would begin by taking the inverse of the +7 which is -7, right? So, technically you are SUBTRACTING 7 which means when you do this equally to both sides of the equation you are using the Subtraction Property of Equality.

 

Hmm…

Step 2: Multiplication Property of Equality

Now, you have now simplified things so you are down to x/3 = 21.

 

The next step is to find the inverse operation where you can isolate the variable, x, from the /5. Since we have a fraction (EEK! The dreaded 'f' word which you learned before is really your BFF) you should have remembered that fractions are actually division problems so if your variable is the numerator, then that means you have been dividing by a divisor so the opposite would be to MULTIPLY! So, by looking at that divisor (3) you now have to multiply both sides of the equals sign by 3, hence, the Multiplication Property of Equality.

 

Easy-peasy, lemon-squeasy!

 

Is this ridiculously simple or what?

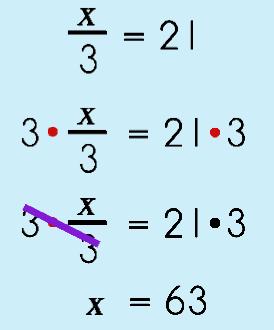©2011–2017 Sherry Skipper Spurgeon.

All Rights Reserved.